El Miércoles día 20 de Mayo encontré un artículo del Sr. Trias de Bes en un periódico económico que reflexionaba sobre un tema que desde el inicio de la pandemia me ha perseguido y quería comentar en algún post: la teoría de juegos. Para mí ha sido inevitable pensar todos estos días, cuando se hablaba de buscar los equilibrios necesarios entre el sistema sanitario y la economía, evocar al Señor Nash y el Señor von Neumann con sus problemas económico-matemáticos de principios y mediados del pasado siglo XX. Muchos de ustedes conocerán la figura de John Nash por la película “Una mente maravillosa” (“Una mente brillante” en América Latina) de 2001, donde Russell Crowe interpretaba a un matemático esquizofrénico de la Universidad de Princeton que ganó el premio Nobel en 1994. Pues bien, este académico americano de altas capacidades fue uno de los sujetos que evolucionaron un problema económico que tenía dos cientos años de antigüedad y que ha marcado, y continúa marcando profundamente, la manera de pensar capitalista hasta nuestros días. Antes de entrar en la materia en concreto, me gustaría decirles si han visto la película, que ni él mismo imaginó la trascendencia que cogerían sus ideas avanzados los años, y hoy parte de sus teorías pueden ayudar a resolver muchos de los problemas a los que nos enfrentamos como el cambio climático. Reflexionar sobre ello es el objetivo de este post.

Es innegable que hay grandes personalidades que han marcado la forma que vivimos y pensamos. Ni que no hayamos leído sus obras, sus teorías tuvieron tal impacto en la sociedad que la han conformado tal y como es. Uno de ellos fue Adam Smith que en 1776 publicó “La riqueza de las naciones”, obra imprescindible para entender como funcionaban y funcionarían los sistemas económicos hasta nuestros días, y es considerado el padre de la economía política. Ni que su obra puede haber sido parcialmente malinterpretada, unos de sus postulados principales proclama que la libre competencia es la forma más eficiente para aportar bienestar a la sociedad y que sus posibles desequilibrios son corregidos por “la mano invisible” de los mercados y el sistema en general. Esta “mano invisible” no es nada más que cada uno de nosotros trabajando mientras primamos nuestro interés individual, y en la búsqueda de éste, los mercados encuentran su equilibrio óptimo. Para la posteridad han quedado los sistemas liberales y neoliberales donde “Mr. Market” dicta las leyes basadas en miles de ciudadanos y empresas buscando su propio beneficio. Los resultados los conocemos, y llevamos noventa años buscando una versión mejorada aunque de momento ha demostrado ser la única alternativa viable. Antes de introducirles las aportaciones de Nash, me gustaría ponerles una escena de la película mencionada donde se emula un posible “momento eureka” de su teoría (el momento es pura ficción y no ocurrió así). Aunque el ejemplo es tremendamente sexista, es muy entendedor. Como reflexión paralela, piensen como en menos de diecinueve años puede quedarse una película tan desfasada en temas de género… (léanlo en positivo). Vean:

Lo que han visto es ficción pura y no fue Nash el primero que cuestionó esta dualidad entre balancear el interés individual y el interés colectivo, Nash fue uno de los principales impulsores de esta disciplina y la ayudó a dotarla de una base matemática más sólida. La teoría de juegos es una disciplina económica que estudia las interacciones de varios entes o “jugadores” dentro un sistema de incentivos. Es evidente que ésto es aplicable a todo, o casi todo, y su complejidad varía en función del número de jugadores, la complejidad de su interacción y la transparencia o existencia de información que posee cada uno de ellos. Por este motivo hay multitud de tipologías de juegos que se estudian por separado: suma cero, simétricos, asimétricos, cooperativos, no cooperativos, combinatorios, etc. El ejemplo más famoso es el “Dilema del prisionero” y del que me ayudaré para explicarles la situación en la que nos encontramos. El dilema del prisionero es la historia de dos ladrones que acaban de ser detenidos y están en la cárcel. La policía les ofrece un trato: “si delatan al compañero, ellos quedarán libres y el otro lo condenarán a diez años de prisión. Si confiesan los dos, recibirán ocho años de condena cada uno; pero si nadie habla sólo estarán un año en la cárcel por imposibilidad de probar los hechos de forma fehaciente”. Se describe en esta forma de matriz:

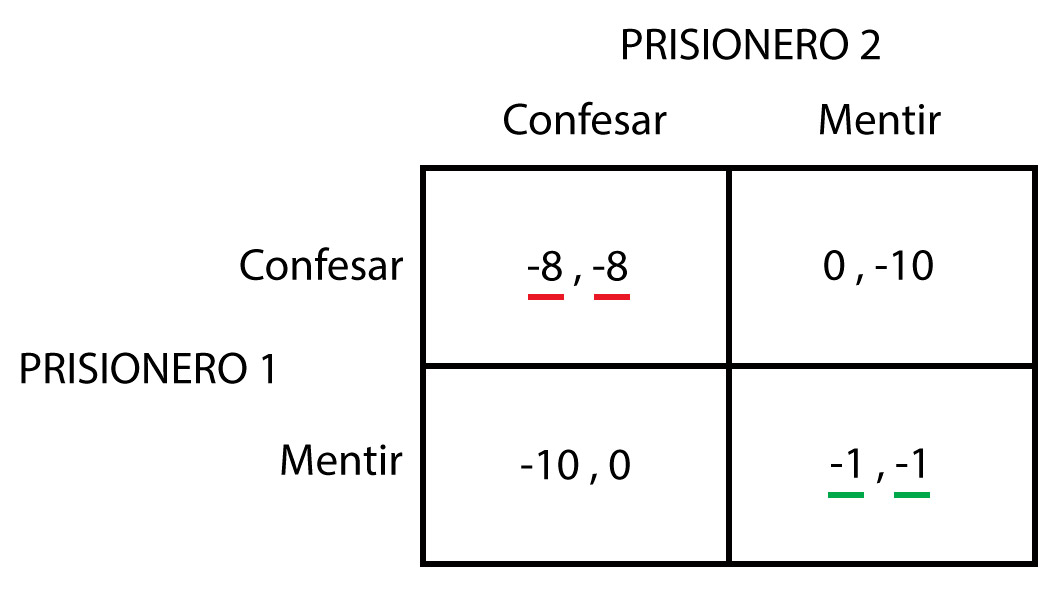
Este juego tiene dos soluciones o “equilibrios” aunque sólo uno es óptimo; la cooperativa donde los dos acuerdan actuar para beneficio de ambos y no confesar, o la no cooperativa donde se traicionan mutuamente. Piense ahora qué cree que ocurriría en su realidad. Mi teoría es la siguiente: los dos prisioneros se encontrarían en el patio de la cárcel y se dirían “si no hablamos ninguno de los dos, en un año estamos fuera, ¿ok?”, así que pactarían esta solución y volverían a la soledad de sus celdas. En medio de la noche uno se levantaría y pensaría: “si éste me defrauda me caerán diez años y él saldrá impune, y seguro que lo hace porque es un traidor; así que voy a delatarle porque, como mínimo, no cumpliré los diez años enteros”. El otro podría pensar de la misma manera en la soledad de su celda. Al día siguiente, a los dos les caerían ocho años de prisión porque se han delatado mutuamente. La solución óptima sólo puede darse si hay un agente externo que se asegura que se consigue lo mejor para el conjunto; en el caso del ejemplo podrían ser “los clanes” de los ladrones. En esta hipotética situación, se dirían en el patio: “si no hablamos ninguno de los dos, en un año estamos fuera, ¿ok? Y si me traicionas cuando salgas mañana mis compañeros se asegurarán de que no vivas para contarlo”, de esta forma los dos conociendo las implicaciones colaborarían y en un año estarían fuera. El señor Nash teorizó sobre “el equilibro de Nash”, que es la solución donde cada jugador está ejecutando el mejor «movimiento» posible, teniendo en cuenta los movimientos de los demás jugadores maximizando sus ganancias (recuerden el ejemplo del video). Lo sorprendente de su teoría es que hay muchos juegos que no tienen este equilibrio, y en el caso del prisionero, intentando maximizar las ganancias individuales, que son 0 años de prisión, caerían en los ocho años de pena. Nash considera el 1,1 un equilibrio inestable dado el riesgo intrínseco de querer maximizar siempre el beneficio individual. Y si no se obtiene el equilibrio de Nash óptimo, lo debemos forzar, buscar un agente externo o un “clan de ladrones” que haga que ocurra. Continuaremos hablando sobre esto.

Vamos a la situación actual, la post-pandemia o la desescalada. Imagínense que, en lugar de dos ladrones, los jugadores son empresarios y trabajadores. Los empresarios dicen: “cómo todo el mundo teme el futuro y hay mucha incertidumbre, voy a despedir el máximo de empleados posibles, bloquearé las inversiones, las subidas de salarios de los que queden, acumularé efectivo y esperaré”, por otro lado los trabajadores dicen: “cómo los tiempos son inciertos y puede que mi trabajo tiemble, ahorraré más, no me compraré el coche que necesito, ni el abrigo, ni me iré de vacaciones y esperaré que pase el vendaval”. ¿Entienden el dilema? Unos por otros arruinan el país y se quedan sin trabajo ni empresas. Puede que la patronal y los sindicatos hagan una reunión con todos los medios de comunicación nacionales y pacten cooperar, apareciendo en primera página de todos los medios el día después. Es decir, unos proclaman no despedir y mantener la inversión. Los otros comprarse el coche e irse de vacaciones. Pero después de la reunión el empresario se sienta en su despacho y piensa “¿y si soy el único que mantiene las inversiones y los salarios, no vendo nada en los próximos meses, y acabo lleno de deudas? Y el trabajador cenando con su pareja deciden: “no nos compraremos el coche porque si nos despiden no podemos pagar la letra ni el cole de los niños”. Todo el mundo maximizando su estrategia y conociendo la de los demás, no gasta un duro, ahorran o despiden y su región se adentra en una recesión de años. El equilibrio de Nash debe evitarse y buscar la solución más inestable pero óptima. Llegados a este punto algún lector podría pensar: un agente externo debe solucionar el problema y asegurarse la cooperación; debe aparecer un “clan de ladrones”. Y la primera respuesta a esta pregunta es: ¡el Gobierno! Si hacemos esta reflexión nos encontramos con dos problemas principales; si nuestro gobierno nos obligara a gastarnos nuestros ahorros, a no poder despedir o a obligarnos a realizar una inversión concreta en maquinaría veríamos nuestras libertades coartadas, nos sentiríamos atacados en lo más íntimo, y además, yendo completamente en contra de las leyes Adam Smith se tomarían decisiones catastróficas ya que no se reflexionarían suficiente sin este sentido de la individualidad y el beneficio personal. El Gobierno puede “incentivar” pero no obligar, e “incentivar” cuesta dinero. Continuamos necesitando ese equilibrio cooperativo que balancee el bien individual con el común, ese equilibrio de Nash que en este juego no existe a menos que se fuerce. En segundo lugar, cabe preguntarse si el Gobierno en lugar de ser una parte externa de este juego no es un jugador más. ¿Ha pensado que nuestros intereses y los del Gobierno pueden ser “distintos” en una recesión? El Gobierno quiere cobrar impuestos, reducir su deuda, tener más funcionarios e influencia y quedar bien para ser reelegidos. Si el empresario piensa en no invertir, despedir y ahorrar; el Gobierno puede estar tentado de hacerlo también. Incentivar con exenciones de impuestos, aplazar cotizaciones y/o contratar más obra pública puede generar un incremento de deuda y mayores problemas en el futuro. Con más deuda en un futuro se verá obligado a recortar, a decrecer, a ser impopular y a perder poder… El Gobierno tiene las mismas estrategias que un jugador más en este juego; puede tener miedo, pensar “que se endeuden otros” y tomar políticas de contención y austeridad, o puede mantener la calma, cooperar en este juego de la recesión, y apostar por un escenario de menos años de sufrimiento. Ya ven que seguramente aquí, como en el dilema del prisionero, la duración de la prisión/recesión son muy parecidos, pero hay más jugadores. Si volvemos a la matriz inicial verán que puede ser exactamente la misma cambiando el confiesa o guarda silencio por gasta o ahorra:

Una vez analizado el problema usted dirá: ¿cómo se soluciona? En primer lugar les diría, que de los tres jugadores de este juego (pueden ser más, como por ejemplo, los bancos que proporcionan liquidez), hay dos que se componen de millones de voces, empresarios y trabajadores, y el tercero es sólo uno, el Gobierno. Por este motivo, éste es más “fácil” de alinear y debe tomar la opción keynesiana de gastar, incentivar, subvencionar para situar al menos un jugador en la parte de la cooperación. Si le preocupa que su Gobierno enfrente esta situación piense que una recuperación rápida es también lo mejor que le puede pasar a nivel impositivo y de deuda pública en el medio plazo. La segunda fase sería como reenfocamos a los dos otros jugadores en la parte de cooperar para que no permanezcan en la de competir contra el sistema. ¿Cómo buscamos el factor externo, el “clan de ladrones”, que haga movernos a todos hacia la casilla de la cooperación? Mi respuesta sería buscar agentes y factores que eliminen el miedo y la incertidumbre. Que el Gobierno se situé de entrada en la estrategia “cooperar” ayuda, y mucho, si se hace bien y distribuye la riqueza adecuadamente; pero faltan más actores. Y aquí es donde sólo puede entrar una sociedad civil más fuerte, más coordinada, que hable de tú a tú con empresarios y trabajadores, y les “convenza” sin invadir su intimidad ni hacerles tomar decisiones que no quieren tomar. La creación de hubs sectoriales con empresas estratégicas en una Región, con un plan común y un liderazgo claro, puede ayudar a que muchos empresarios crean en la oportunidad que se esté creando para invertir con fuerza. Que Universidades de prestigio formen a talento local para poder generar modelos de más valor añadido y de más productividad en una Región ayuda a mantener la confianza de encontrar soportes para los proyectos que se emprenden. Que agrupaciones vecinales se coordinen para promover un modelo de ciudad o pueblo más adecuado para sus intereses y los de sus hijos pueden accionar la motivación para continuar residiendo en ellas e impulsarlas. Y sobre todo, líderes que den un primer paso, que aglutinen consensos civiles y políticos y den ejemplo con inversión y gasto, deben ser la estocada para que el miedo no se enquiste en la sociedad y decidamos no agazaparnos para afrontar años de travesía en el desierto. Pasar del modo “competir” al de “cooperar” es cuestión de confianza, buscar soportes y combatir los miedos de forma conjunta. Porque si algo tengo claro, es que todos los jugadores de este tablero ahora mismo los tienen.

Para completar la reflexión, les aseguro que la literatura de la teoría de juegos cuenta hoy con múltiples conceptos ya establecidos y múltiples estrategias para abordar problemas reales con modelos matemáticos complejos. Hay tipos de juegos que no tienen solución y otros que son fáciles de determinar. Para definir el problema a menudo se deben definir dos conceptos claves (hay también alguno más que obviaré): de qué tipo de juego se trata, y tipo de estrategias dominantes que utilizarán los jugadores. Me gustaría definir claramente el que nos ocupa:

• Tipo de juego: Si el juego tiene unas reglas claras y se rige por un “contrato” el juego es cooperativo, ya que los jugadores deben colaborar por las leyes que les subyacen. Si los jugadores priman maximizar sus ganancias en el juego conociendo la situación de los demás, y no hay leyes escritas posibles, es no-cooperativo y debemos buscar el equilibro de Nash o forzarlo. ¿Qué tipo de juego es la post-pandemia? Lo han adivinado, por desgracia las leyes que deberían regirnos, el “contrato social” entre agentes existente algunas décadas atrás parece estar roto ya que la mayoría NO se considera ligado moralmente a actuar en consecuencia por el bien común. Los agentes deciden maximizar sus posturas y todos juegan contra todos; los empresarios contra los Gobiernos, los trabajadores contra los empresarios o los Gobiernos contra los trabajadores. Sin agentes externos, ante la imposibilidad, siendo coherentes y por el bien de todos, de poder utilizar leyes que rijan lo más privado, el juego puede no tener solución o no llegar nunca a la solución óptima. Es el dilema del prisionero. Como idea, sólo la UE en Europa, parece estar jugando el papel del «clan de ladrones».
• Estrategias dominantes: son las decisiones que cada uno de los jugadores puede elegir. Si una estrategia es estrictamente dominante quiere decir que el jugador siempre utiliza la misma estructura de decisión independientemente de qué hagan los demás. Es lógico pensar que los jugadores que deciden jugar de esta forma acaban perdiendo en el largo plazo. A menudo se ponen nombres a las estrategias: estrategia egoísta o estrategia cooperativa, pudiendo un jugador elegir entre las dos a medida que avanza el juego y dispone de más información. ¿Qué estrategia ha decido jugar usted? ¿Egoísta puro?, ¿Cooperativo hasta que vea que deba cambiar a egoísta? o ¿Cooperativo puro dispuesto a mantener su estrategia hasta el final por el bien global? Si todos formamos parte de este juego es lógico decidir cómo nos vamos a posicionar y qué condiciona nuestra posición, y en este caso puede que nunca lleguemos a una solución óptima para todos los que formamos parte de esta partida: la sociedad en general.

Si buscan juegos donde los jugadores no cooperan y las estrategias tienden a ser egoístas encontraran otro caso «de libro» dentro la teoría de juegos: “La tragedia de los comunes”. Su nombre es ya suficientemente explícito. El caso explica uno conjunto de granjeros que deciden compartir un campo excedentario para el pasto de sus vacas. El campo y su hierba es un recurso limitado, y como su título indica pueden imaginarse cómo acaba… Con ésta última reflexión les quería mostrar que, sin cooperación alguna, con estrategias egoístas en juegos no-cooperativos por definición todos acabamos perdiendo dado la imposibilidad de encontrar la solución correcta. La gran aportación de John Nash es que ayudó a teorizar, pensar y calcular soluciones con estrategias distintas a las planteadas por Adam Smith, donde “la mano invisible” egoísta hacía que nunca se llegara a un óptimo común creando grandes desigualdades. Nash aportó una idea brillante a nuestro mundo: “podemos cooperar y optimizar/maximizar los resultados para todos los participantes”. Puede que el problema de la post-pandemia no sea de recursos finitos ya que se puede imprimir dinero indefinidamente y encontrar “soluciones válidas” menos optimizadas; pero si piensan en el siguiente problema, el cambio climático, si no hemos solucionado las estrategias de cooperación entre los agentes de la partida, verán como la Tierra acaba como el pasto de nuestros granjeros en la tragedia de los comunes… Piensen en ello, busquen ser parte de la solución, encontrar un «clan de ladrones» y tomen sus decisiones.